|
Доказательство. Покажем сначала единственность. Предположим, что существуют два вектора 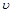 и и 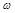 , удовлетворяющих соотношениям (7). Пусть , удовлетворяющих соотношениям (7). Пусть 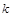 - номер компоненты, для которой - номер компоненты, для которой
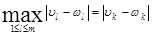 , ,
и пусть для определенности 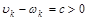 . Определим две матрицы . Определим две матрицы 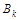 и и 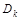 следующими соотношениями: следующими соотношениями:
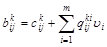 , ,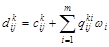 . .
Очевидно,
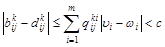 . .
Из леммы 1 следует, что
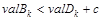 . .
Поскольку 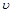 и и 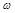 удовлетворяют (6) и (7), то удовлетворяют (6) и (7), то
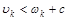 , ,
что противоречит предпосылке 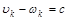 и доказывает единственность. и доказывает единственность.
Докажем существование. Доказательство конструктивное, основанное на построении последовательности векторов, сходящейся к требуемому вектору. Пусть 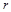 - номер члена последовательности. Определим члены последовательности следующими соотношениями: - номер члена последовательности. Определим члены последовательности следующими соотношениями:
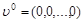 , (8) , (8)
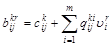 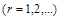 , (9) , (9)
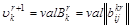 . (10) . (10)
Требуется доказать: 1) последовательность векторов 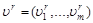 сходится; предел этой последовательности удовлетворяет условиям (6), (7). Положим сходится; предел этой последовательности удовлетворяет условиям (6), (7). Положим
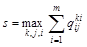 . (11) . (11)
Поскольку выполняется (2) и множества индексов 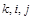 конечные, то конечные, то 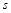 существует и существует и 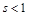 . .
Если положить
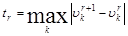 , ,
то по лемме 1 следует, что 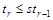 и, следовательно, и, следовательно, 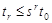 . Поэтому согласно признаку сходимости Коши последовательность . Поэтому согласно признаку сходимости Коши последовательность 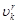 должна сходиться к пределу, который обозначим через должна сходиться к пределу, который обозначим через 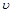 . .
Пусть теперь
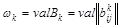 , ,
где
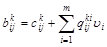 . .
Покажем, что 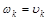 для всех для всех 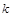 . Действительно, на основании сходимости последовательностей . Действительно, на основании сходимости последовательностей 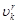 для любого для любого 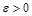 можно выбрать можно выбрать 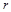 столь большим, что для всех столь большим, что для всех 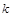 выполнялись неравенства: выполнялись неравенства:
|